NP-complete problem may enable startup founders to convince counterparts without delivering any knowledge

the nature of P versus NP (P=NP, P≠NP) problem
What a startup is proving by fundraise
Here is the statement I am checking if this is true and can be applied to technology startup journey throughout my career as both an entrepreneur and investor.
“Startup can convince counterparts without disclosing any information if the startup have true theorem that carries a zero-knowledge proof, NP-completeness. “-Shoichiro Tanaka, HITSERIES CAPITAL
The counterparts will be either customers, partners, employees, investors or society. If the prover has true theorem then the truth with NP-completeness will gather all the caluculating powers to prove the theorem: asset, energy, resources, materials, human intelligence. It may influence all over the world and accumulate calculating force from all over the world and make that startup competitive;which looks as super gravity power.
Caluculating powers can be attracted to the center of startup in a necessary manners, orders and timings. The management of startup just picks it up or filter the information by true value. It will not requires tough negotiation, only easy conversation will be required to make that true startup grow.
The power of the true startup to accumulate resources (funds, people, computing power, energy) is the power of truth. If the true theorem posed, someone will start to verify it, follow proof, experimenting reproducibility, repeatability, duplicability of the posed theorem.
One of the HITSEREIS CAPITAL(TANAAKK) slogan, Η ΑΛΗΘΕΙΑ ΕΛΕΥΘΕΡΩΣΕΙ ΥΜΑΣ (The truth shall make you independent) is true theorem that can be verified at once and require a long long time to be proved.
HITSERIES CAPITAL think, a fundraising startup should have clear theorem behind how it solve the world’s problem. Every successful startup should have the initial thesis verified as true by small audience but yet to be proved as true to be theorem by mass computational calculation and people’s intelligence.
To understand this statement, we must understand the history of computer science and mathmatics.
What is a proof
I’ll try to explain what zero knowledge proofs are and maybe why they are also useful. Proof is the basis of mathematics. The way we know that something is absolutely true is by proving it. We know that every numerical materials can be 1+1=2. We can prove it and then we know that this is true for everything we meet even some we didn’t meet. Every one apple and one apple can be added to 2 apples. Proofs are what make us certain about certain mathematical facts. But if we prove it, we have to prove there is no any matter or anti-matters that cannot be 1+1≠2. We cannot observe whole universe. So 1+1=2 seems to definitely true and easily verified, but the proberbility is 99.999999999999999….%, not equals to 100%. It is easy to find, but difficult to check the truth.
How to get certainty that a proof have true value
What makes it they’re certain about it is that they are convincing they follow this logic that, any person wants to verify the proof can just follow the steps of the proof and be convinced that it is indeed true.
You can show a pen. a pen plus a pen will be 2 pens. You can show a card, one card plus one card is apparently 2 cards. This truth seems easily verified but this truth is not checkable if we cannot clear if there is not exception of the law of conservation of mass in the universe. (Some scientists assume in blackhole there may be exception of the law of conservation.)
So 1+1=2 seems apparent and easy to find(P), but it will not mean it is easily checkable(NP)
P(polynomial time solvable problems)≠NP(nondeterministic polynomial time verifiable problems)
Most computer scientists believe P is not equal to NP (P ≠ NP). This would mean there are some problems that are easy to verify but very difficult to solve.
In computational complexity theory, P, also known as PTIME or DTIME(n), is a fundamental complexity class. It contains all decision problems that can be solved by a deterministic Turing machine using a polynomial amount of computation time, or polynomial time
Verifier can check the validity of the proof without any evidence
To someone who didn’t know it was true in advance – verifier of the proof – there’s a way to check even if he didn’t know a proof to check given a proof that it’s correct and usually it’s much simpler than proving a theorem right.
In the startup ecosystem, lead investor should be verifier of the startup’s proof of concept. (it’s only ideal and not working so clearly in the real world)
The prover, the guy who proved it, like British mathematician Andrew Wiles who proved the Fermat’s last theorem, he wrote down a proof and then people with some amount of work, but not much need for ingenuity, could verify that it’s correct. That is to say, if the proof have true value, verifier can check it is correct even if he or she does not know a proof to check. Usually verification work is much simpler than proving a theorem itself right.
Zero Knowledge Proofs
Zero knowledge proofs are proofs that reveal absolutely no information to the verifier. Imagine a startup founder is a prover that knows some truth and some proof of it maybe a mathematical theorem. (mathematical theorem means that can be solved by computing power, turing machines, which definitely required for startup founders that are raising money from technology VCs.)
Given that verifiers would not be fooled by any nonsense. If the claim is false, if the startup doesn’t have a proof for it the claim should not be convincing.
On the other hand, if the claim is true, the process in a zero knowledge proof should be convincing.
How Zero Knowledge Proof works
How zero-knowledge proof works? Prover want to convince verifier. There should be some conversation between two parties, at the end of it, a verifier know nothing more than the verifier knew before except that the claim prover made was true. There’s no information about the proof in this conversation. (for example, what early stage startups are telling is all “plan” no real track records, there is no real information about truth. But if the prover beforehands proved that their theorem is right, the verifier will pass it as true)
There is no information about anything in fact that the verifier didn’t know. and nevertheless there is no way to fool the verifier and the verifier will be convinced. The prover cannot trick the verifier into believing something incorrect or something the prover don’t have a proof of it. (in the real world, scammer or failing startup; the prover that does not have truth value of proving theorem can raise some money but it will turned out be false after mass culculation by people intelligence)
After the prover(a startup founder) convinced the verifier(an investor), the verifier has no new information gain except for the prover’s theorem is true.
Theory and Theorem
Every theorem is a theory but not every theory is the theorem.
A theory consists of some basis statements called axioms, and some deducing rules (sometimes included in the axioms). The theorems of the theory are the statements that can be derived from the axioms by using the deducing rules.
- Theory: A broad concept explaining some phenomenon or area of study. It provides a framework for understanding how things work based on assumptions and rules. Theories can be based on evidence, logic, or a combination of both. Scientific theories, for example, are constantly refined as new evidence emerges.
- Theorem: A specific statement proven to be true within a particular theory. Theorems are derived from the accepted truths (axioms) of the theory using logical reasoning and established rules. In mathematics, theorems are the cornerstones of different branches, like the Pythagorean theorem in geometry.
If the prover have theorem, then there will be the way for verifier to check it as true by zero knowledge.
The power of zero knowledge proof
Let’s say you just proved the Riemann Hypothesis, which is a long-time unproven theorem. This is maybe the most famous problem in mathematics. And you at first consult it to your senior professor. The professor says show me how the proof goes. You will start using the board or your brown paper and start showing the lemmas and the proofs and the whole sequence. Maybe it will take an hour, maybe it will take a day or maybe it will take a year.
But if you know zero-knowledge proof, if you had the proof, the professor will be convinced without providing any knowledge. There are a few stories in the history of mathematics – some of which you may know – where the senior guy, having heard the proof, rushed and published it. The theorem may be stolen by not using zero knowledge proof. It’s not that it happened often, but in the long history it happened. So maybe the junior guy, prover, would like some protection. It would be much better if the prover could convince the verifier completely that the prover have a proof of the Riemann Hypothesis without giving the verifier a shred of evidence besides that you know that it’s true. So that’s the value for a zero knowledge proof.
How to distinguish truth
So now you should ask yourself which mathematical statements, or which statements at all, have such proofs without knowledge? You want to know truth. It seems counter-intuitive to say, because we somehow associate conviction with information transfer.
That is given truth in society, If there’s no information, if I didn’t learn anything new but I verified and accept it. (e.g. you are breathing the air around you without any doubt.)
Zero knowledge proof in VC industry
So in the world of startup and venture capital, if an investor doesn’t know the startup’s proof algorithm to reaching absolute certainty, but VC can know the founder is telling the truth. There is the way the founder can convince the investors to verify and believe in the startup even if they do not know anything.
“I think a simple rule of business is, if you do the things that are easier first, then you can actually make a lot of progress.” — Mark Zuckerberg.
So to go back to Riemann Hypothesis, if you solve it, instead of writing down infinitely many primes, you can expect it would be finite and publish it right. Should ask yourself what kind of statements at all can have such proofs(=zero knowledge proof).
Every statement which has a proof has a zero knowledge proof
“Every statement which has a proof has a zero knowledge proof.”
The question was raised in the context of cryptography by Oded Goldreich, Silvio Micali and Avi Wigderson in the mid 1980s about a year later they proved that.
Oded Goldreich, Silvio Micali and Avi Wigderson How to construct zero-knowledge proof systems for NP
Zero-knowledge proofs are probabilistic and interactive proofs that efficiently demonstrate membership in the language without conveying any additional knowledge. The wide applicability of zero-knowledge was demonstrated in Proofs that Yield Nothing But their Validity or All Languages in NP have Zero-Knowledge Proofs, coauthored by Goldreich, Micali and Wigderson [JACM, July 1991]. In particular:
- It is shown that Graph Isomorphism and Graph Non-Isomorphism have (perfect) zero-knowledge proof systems.
All previously known zero-knowledge proofs were for sets related to number theory, and furthermore GNI was the first set not known to be in NP that was shown to have an interactive proof system. - Assuming the existence of one-way functions, it is shown that every language in NP has a zero-knowledge proof system.
Only few sets were known before to have zero-knowledge proofs and so the utility of zero-knowledge was previously restricted to some special cases. In contrast, this result asserts that zero-knowledge exist for any statement having an NP-proof. The dramatic effect of this result on the design of cryptographic protocols is demonstrated in another paper of the same authors; see webpage on How to Solve any Multi-Party Protocol Problem.
How to Solve any Multi-Party Protocol Problem
Assuming the existence of trapdoor permutations, one can construct protocols for securely computing any desirable multi-party functionality. This result either require a majority of honest players or allow dishonest players to suspend the execution (while being detected as bad). In the former case, the protocol can tolerate adversarial behaviour of any minority, and no minority can learn from the execution more than it can learn from its own inputs and the value of the function. In the latter case, the only additional damage that the adversary (which controls half or more of the parties) can obtain is prevent the honest parties from obtaining the output value (but the adversary’s decision is oblivious of the inputs of the honest parties). Loosely speaking, in both cases, the protocol simulates a trusted party in an environment in which no party can be trusted.
Application of zero-knowledge proof
So we can apply it with startup theorem, we can do it with the Riemann Hypothesis, every statement which has a proof also has a zero knowledge proof. But I just want to say that this zero knowledge proof will be slightly different than normal proof you just write it down – in a zero knowledge proof we need to interact. You need to ask me questions and it is interaction. Zero knowledge proofs are interactive.
The verifier can interact with the prover without increasing the verifier’s knowledge. But the prover can refuse to answer any questions the verifier like to know and then the verifier will get no knowledge.
The nature of proof
This is the nature of proof. Giving proofs in an interactive setting, even if you didn’t get an example or whatever you can be convinced. So interactive proofs is a natural object. We can think how do we even check the certainty that gave no information if the proof has truth value. Proving something is zero knowledge means what you are proving is truth.
How to deliver truth
There is some technique to use to deliver truth.
- First we proved that a certain type of statements, which is very pictorial, has a zero knowledge proof – four colour theorem –
- If you have a proof it has a zero knowledge proof – and then we appeal to a general result about the NP(nondeterministic polynomial-time) completeness of this problem.
This is an important concept in computational complexity, to derive from that that every statement which has a proof has a zero knowledge proof. Nondeterministic Turing machine
It’s a very famous theorem in mathematics that every planar map like this one can – no matter how many countries it has – can be coloured with four colours. not every map can be coloured by three colours. But if we use envelop and limit verifier’s action only opening 2 countries envelope in a same time like memory game in trump card, then, we can only use 3 colors. it is limited proof. but there will be more meta layer of proof (every countries can be colored by 4 countries.)
Like this, real startup truth is concealed by limited thesis or theory that cannot be theorem.(cannot be self-verified, cannot be proved with zero knowledge) They would be luckey by concealing multiple countries by envelope but if there was infinite times action then the false evidence will be revealed after some time.
if I had a proof that you will not only see two different colours, you’ll see two random different colours and you’ll see just a random pair from this column, but it’s something you could have done yourself. If I had a proof you will learn nothing because the process will just reveal pairs of random colours. If I didn’t have a proof(that you will not only see two different colours), you would catch me cheating because countries cannot be coloured by 3.
statement can be converted into a map and I should stress this conversion is efficient there is a simple algorithm known to all, it’s a result from the late 1970s – a fundamental result by independently by Cook and Levin – they basically prove that any mathematical statement that’s formal can be written down can be converted into a map and this translation between the statement to a map is very simple, efficient, known to everybody.
Summary
This NP completeness is a fundamental point. Having an NP completeness, having an NP complete problem is so elegant. Combinatorially convenient is essential for us to devise this proof.
It’s a standard language which is extremely useful for demonstrating things that in another context look impossible. The main use of NP Completeness is just a demonstration of difficulty of this problem
1.If you had a proof or mathematical statement, every statement could be converted to a map in a way that preserves truth
2. that three colouring maps captures every mathematical statement, so for this reason proving mathematical theorems in general is as hard and as easy as just three colouring maps
It’s not an equation it’s an algorithm. Equations and algorithms are both fundamental tools used for problem-solving, but they approach things in different ways:
- Equations represent relationships between variables. They typically express a single outcome based on the input values. Imagine an equation like y = mx + b, the familiar slope-intercept form for a line. This equation tells you the relationship between the slope (m), x-intercept (b), and the y value for any point on that line.
- Algorithms are step-by-step instructions that define a process for achieving a specific goal. They take an initial input and manipulate it through a series of well-defined steps to arrive at a desired output. Following a recipe is a good example of an algorithm – it breaks down the cooking process into steps to achieve the final dish.
What Cook and Levin looked into SAT (Boolean satisfiability problem) , understood that you can take the verification process of proofs and convert them – the statement and the proof and the process – convert them to (e.g.)three colouring maps that are simple problems that capture all such processes. Localities of computation is what’s essential in this translation so they start from an abstract verification of a proof and they generate from it this map. That’s what the algorithm does – again it’s simple once you know what you want to do – it’s a great idea and an amazingly powerful to use NP completeness and zero knowledge proof.
Diaglam
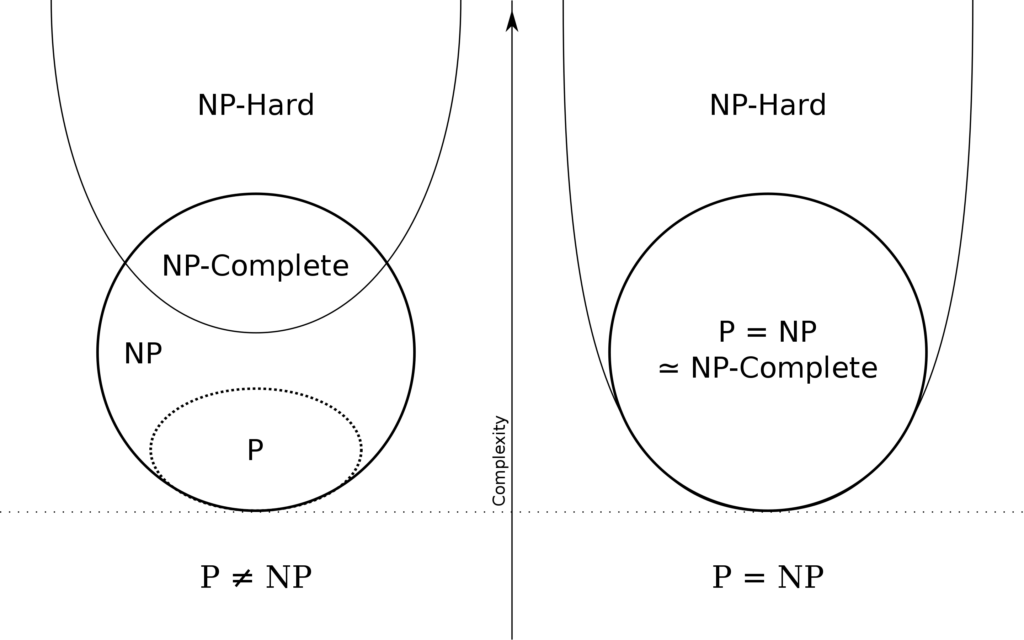
Euler diagram for P, NP, NP-complete, and NP-hard sets of problems. The left side is valid under the assumption that P≠NP, while the right side is valid under the assumption that P=NP (except that the empty language and its complement are never NP-complete, and in general, not every problem in P or NP is NP-complete).
References
P vs NP Clay Mathematics Institute
Bitcoin: A Peer-to-Peer Electronic Cash System
ACM A.M. Turing Award Honors Avi Wigderson for Foundational Contributions to the Theory of Computation
Zero Knowledge Proof with Avi Wigderson

